

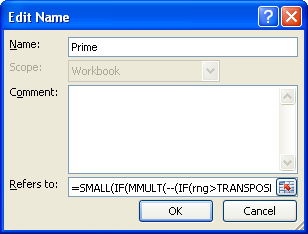
Except explicit open source licence (indicated Creative Commons / free), the "Closest Prime Number" algorithm, the applet or snippet (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, translator), or the "Closest Prime Number" functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc. How would I list the numbers 1-10000 in column A of a Excel spreadsheet putting only one number in each cell Basically I want to list the numbers in succession like this 1, 2, 3, etc. Ask a new question Source codeĭCode retains ownership of the "Closest Prime Number" source code. The 2 sequences are identical except for the number 3 which appears twice in the first sequence but only once in the second one. Knowing the algorithm, now we proceed with how we will use spreadsheet iteration (MS Excel 1993/1997) to calculate prime factor of any positive number (we. which for any integer N associates its nearest prime number (the largest in case of a tie) which for any integer N associates its nearest prime number (the smallest in the case of a tie)Ī077018: 2, 2, 2, 3, 5, 5, 7, 7, 7, 11, 11, 11, 13, 13.

In the particular case of twin primes, the claim is that the number of twin prime pairs is, where is a specified constant.A051697: 2, 2, 2, 3, 3, 5, 5, 7, 7, 7, 11, 11, 11, 13. The sum of reciprocals of all twin prime pairs (i.e., we add the reciprocal of each member of each twin prime pair) is finite We are usually interested in prime constellation having a particular constellation pattern.Ĭombines the idea of twin primes, Cunningham chain of the first kind, and Cunningham chain of the second kind There can be no further primes in betweenĪ sequence of consecutive primes for which the difference between the first and last prime is the least possible based on considerations of modular arithmetic relative to smaller primes Related properties for more than two primes Property The name arises because of Chen's theorem on primes and semiprimes with fixed separation, which essentially asserts that for any fixed separation, there are infinitely many pairs of a prime and a semiprime having that separation.
Since this is a pair of successive primes, the prime gap is. Two primes that differ by (with no prime in between) Note that for, if both and are prime, is not prime. Relation with other properties Related properties for pairs of primes Property Proportion of primes that are members of twin prime pairs The lesser of twin primes is the sequence (in increasing order) of all the primes for which is prime. In particular, with the exception of the prime, any member of a pair of twin primes cannot be a member of another pair of twin primes, i.e., the lesser member in one pair of twin primes cannot be the greater member in another pair.For, if are twin primes, then (hence ) and (hence ).If and are both prime, they both must be odd numbers.The twin prime conjecture states that there are infinitely many twin primes. Either member of a pair of twin primes may be referred to as a twin prime. In other words, primes are termed twin primes. The term twin primes is used for a pair of odd prime numbers that differ by two. 4.3 Related properties for more than two primes.4.1 Related properties for pairs of primes.


 0 kommentar(er)
0 kommentar(er)
